This paper demonstrates a simulink model based on mathematical model of the Electromagnetic magnetic levitation system. The state equations of magnetic levitation spherical driving joint To using state space model system magnetic levitation.

Magnetic Levitation system is an unstable and sensitive system.
Mathematical modeling of magnetic levitation system. The formula 3 can describe the dynamic mathematical model of the magnetic levitation spherical driving joint without regard to the factors of the winding. Thus the system is the nonlinear strong coupling system. The state equations of magnetic levitation spherical driving joint To using state space model system magnetic levitation.
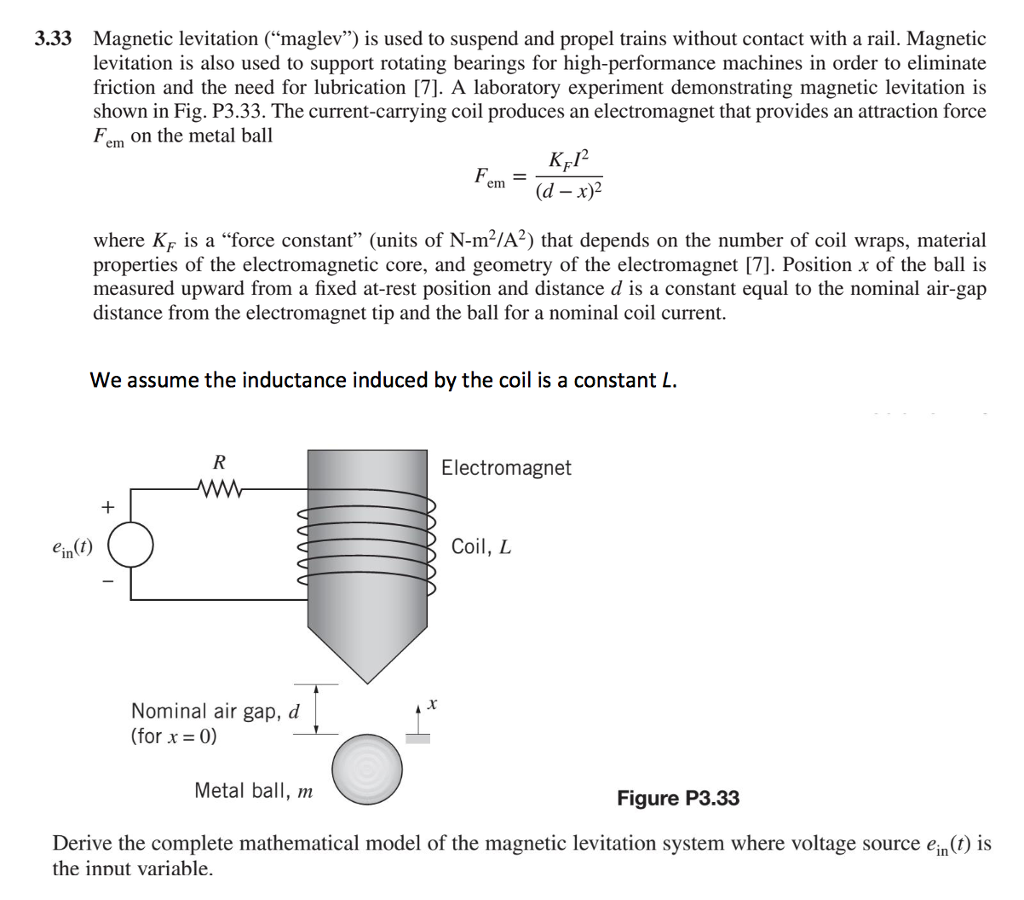
The mathematical model of the Magnetic levitation system is divided into five subsystems namely ball and coil power amplified position sensor and AD and DA converters. K T i a i k u DA 0 u MU u k y x 0 x k AD MUy 0 y MU 0 y sensor k c m k F g F a F m g k fv x0 ball and coil AD converter DA converter power amplifier Figure 2. Magnetic levitation model The mathematical model of the ball and.
This paper presents the mathematical modeling of the magnetic levitation system. Since magnetic levitation system is a non-linear system it is controlled using Proportional Integral Derivative PID controller and Fuzzy Logic controller. The PID Fuzzy Logic and Fuzzy-PID control techniques will be simulated and compared to determine which one of them give the best control performance to the.
Free body diagram of magnetic levitation system. 2 where R is the resistance of the coil L is the inductance of the coil v is the voltage across the electromagnet i is the current through the electromagnet m is the mass of the levitating magnet plus one-forth of the mass of the acrylic plate g is the acceleration due to gravity d is the vertical position of the levitating magnet measured from the bottom of the electromagnet f is the force on the levitating magnet. Modeling the magnetic levitation system belongs to challenging tasks since besides nonlinearities we have to cope with open-loop unstable system with fast dynamics and very small degree of natural damping.
The basic control aim is to precisely position the levitating object which requires adequately precise model. This paper demonstrates a simulink model based on mathematical model of the Electromagnetic magnetic levitation system. A mathematical model showing the dynamic system of equation is represented in the beginning.
The nonlinear parameter inductance that varies with position is stated and analyzed with Matlab. Action of the suspension controller for the magnetic levitation system. As shown in Figure 2 the magnetic levitation co ntrol system consists of a suspension controller a gap sensor and an actuator which is the electromagnet.
The gap sensor measures the gap between. In the linear control design method linearization is often the first step in the control system design and modeling of the magnetic levitation system. It is generally considered that the nonlinear equation is linearized as long as the Taylor expansion is used 14.
Magnetic levitation system has inherent instability thus it requires feedback control. 6 designed the nonlinear maglev model into the Matlab Simulink and designed control algorithm together with simulation model of the Magnetic levitation and. Magnetic Levitation system is an unstable and sensitive system.
High precision force balance condition is required to levitate an object in the air. Accurate mathematical modeling transfer function derivation linearization and appropriate choice of the controller parameters play an instrumental role in the successful levitation of the object. Model of the magnetic levitation system The magnetic levitation system considered in this paper consists of a ferromagnetic ball suspended in a voltage-controlled magnetic field.
Mathematical model of a levitation system based on eddy currents Abstract. This paper contains a synthesis to model an electromagnetic levitation system using a direct evaluation method of electromagnetic and electromotive forces taking the Maxwell equations that relate electric and magnetic. Model a Magnetic Levitation System In this example we attempt to build a neural network that can predict the dynamic behavior of a magnet levitated using a control current.
The system is characterized by the magnets position and a control current both of which determine where the magnet will be an instant later. Thus the state-space model of the magnetic levitation system can be written as dx 1 dt x 2 dx 2 dt g c C m x 3 x 1 2 dx 3 dt R L x 3 2C L x 2x 3 x2 1 1 L u. 23 The state-space model of the magnetic levitation system 23 will be used in the design of the SMC schemes.
Let x 1d x 2dandx 3d be the desired values of x 1 x 2andx 3 respectively. The plant model is controlled by a PID controller with feed forward to cope with the nonlinearity of the magnetic levitation system. The position of the ball responds to the changing value of the setpoint.
You can observe this change not only in the Scope window but also in a. Development of a Magnetic levitation model The nonlinear physical model of the MLS can be described by state equations obtained from basic physical laws for a ball. Annonse More than 2900 Journals.
Springer Offers Many Opportunities for Authors to Publish. Let the World Learn About Your Work. Publish Your Research in Our Journals.